Development of effective method of protection of software and file source codes, located on third- party servers through vigenere encryption

In article the method of protection of the information developed by authors, based on use of Vigenere is considered. Mathematical models for block coding of the information, and also methods and algorithms of their decoding are offered. Modified Vigenere algorithm presented in work with application of the block enciphering, based on a variation of quantity of iteration with key displacement, allows, unlike known algorithms, it is more reliable to protect data on Web - a server.

For encryption of data located on servers different cryptographic algorithms are used: generators of quasi-random numbers, DES algorithm, Vigenere cipher, RSA algorithm.

Effective methods of protection are based on classic model of cryptography, for which it is peculiar to use one secret unit – key. The key allows the sender to encrypt the message, and the receiver – to decrypt. In case of encryption of data kept on magnetic and other information carriers, the key allows to encrypt the information during its recording on the carrier and decrypt during its reading from the carrier.

The most widespread methods of symmetric encryption are DES algorithm and Vigenere cipher.

Vigenere cipher is a method of polyalphabetic encryption of literal text using key words.

DES algorithm encrypts 32, 64 or 128-bit data blocks using key sized from 0 to 2040 bits.

Decryption in DES is the operation opposite to encryption and is conducted by repeating encrypting operation in the opposite order. The process of encrypting is that at first bits of 64-bit blocks are rearranged, encryption in sixteen cycles is conducted, and bits are rearranged again.

It should be mentioned that the tables used during encryption process are standard and consequently have to be included in realization of algorithm in permanent way.

Vigenere cipher needs keeping of one key set by a kit of b letters. Such kits are subscribed repeatedly under the message and then received sequence is summed with the open text on n module (alphabet capacity).

Encryption is conducted as follows:

The base of proposed protection method is Vigenere cipher as it is the most simple algorithm of symmetric protection.

In order to achieve the objective multiple iteration is proposed under which respective algorithms of encryption and decryption consist of consequential single-type cycles of encryption.

Let us use protection method according to Vigenere algorithm and its modifications which use protection methods without feedback, as using of methods with feedback is impossible if there is a noise in communication link, because change of one bit in encrypted message leads to error in decryption of the whole message. This leads to the situation when it is required to request the whole message again, which causes time consumption and occupation of communication link.

The use of block codes allows conduction of half decryption to receive the information about the file. This allows shortening the server's workload when it is used by large number of servers. In order to keep this advantage, it is proposed to use the principle of block coding when modifying the Vigenere code. With the size of the block equal to eight bits, it corresponds to the Vigenere cipher if the alphabet sized n=256 is used. All types of files with all size may be encrypted by the alphabet shown in Table 1. The first line of the table is the direct alphabet, while other lines are shifted on one element.

65

However, this approach doesn't solve the problem of correspondence of blocks of opened and encrypted messages. For example, in encryption indicated in Table 2:

Table 2 -Fie encryption example

There is a problem of mismatch of encrypted and opened file because the use of same bits in opened file allows restoring opened key.

In order to solve the problem the use of multiple iteration method during encryption and decryption is proposed. In order to increase cryptographic security, the key is shifted on the second and further steps of iteration. The shift is calculated based on the remainder of the key from the previous iteration.

Direct process of encryption-decryption appears in the following order. The first step is according to Table 2, the further steps according to Tables 3-5. In this step of encryption the encryption key from the previous step is used as an opened file, and the opened key is shifted on the length of remainder from the previous step.

Table 3 -Second step of encryption

Table 5 -Fourth step of encryption

Comparison of the data revealed in Tables 3-5 with the data revealed in Table 2 shows that starting from the second step the problem of mismatch of bytes in opened and encrypted file is eliminated. This leads to inability of finding out the privacy key by the broaching of possible word. At the same time,

starting from the fourth step different bytes of the opened file may give the same bytes of encrypted file, which makes it more complicated to identify the privacy key using private analysis methods.

For N - iterative encryption it is necessary to pass initial file N times. During direct approach it is applicable, but the same time the ability to use this algorithm for block encryption is lost. Let's summarize the method of block encryption. Block cryptosystems divide the text of the message on separate blocks and then reorganize these blocks with the help of the key.

For block cipher we have to change multiple pass of initial file on encryption by blocks by one byte apart from other bytes in the file.

At the same time each block will be encrypted in several passes with the use of different bytes of the key, and positions which are calculated.

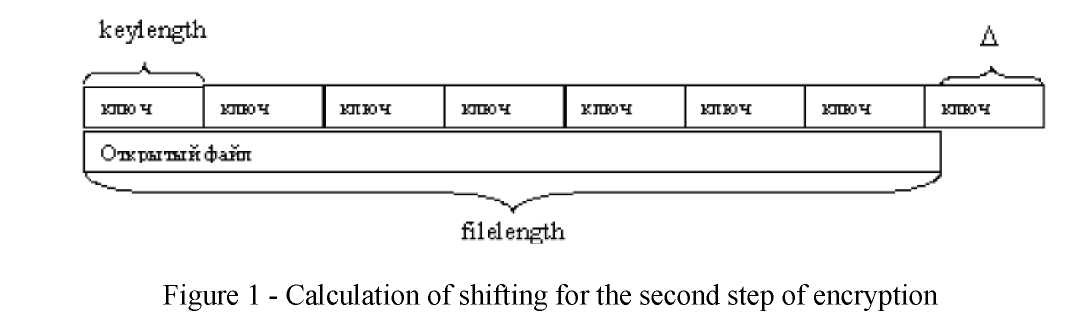
In order to receive the equation used during calculations, we consider the initial shift which is equal to zero, which corresponds the first step of encryption indicated on Figure 1. Using the remainder of the key, we calculate the initial shift for the second step of encryption.

where filelength - amount of bytes in the opened file;

kekeylengt- amount of bytes in the encryption key;

Δ - size of the key shifting at the second step of encryption.

Basing on the above one may conclude that: Δ = filelengthmod kekeylengt.

This shows that the remainder of the key which transits to the second iteration identifies the shift of the encryption key.

Calculation of the shift at every step of encryption is shown in Figure 2.

67

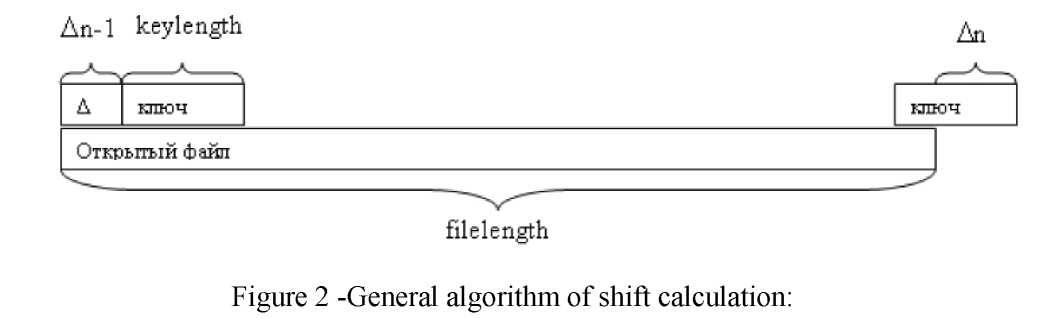
∆_n = (filelength - (kekeylengh - ∆_и_ɪ)) mod kekeylengh

where ∆_n - calculated value of key shift at the n step;

∆ _n-1 - value of key shift at the previous step (n-i)

Based on the above one may conclude that the length of the key is undefined, and in case if

∆ = filelengthmod kekeylengt= 0.

In order for the second and further iterations not to be conducted in vain, it is necessary to shift the key on T bytes. T number is the value defined during the installation of the cryptosystem.

Conclusion

Based on the above, proposed modified Vigenere algorithm with applying of block encryption which is built on variation of the amount of iteration with the key shifting, unlike other well known algorithms, allows to protect the data on web servers better.

BIBLIOGRAPHY

1. Альферов А.П. Основы криптографии. Учебное пособие - Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. [Текст] // 2-е изд., испр. и доп. - М.: Гелиос АРВ, 2002. - 480 с.
2. Панасенко С.П. Алгоритмы шифрования. // Специальный справочник. СПб.:БХВ-Петербург, 2009. - 56с.
3. Thomas W. Cusick, Pantelimon Stanica. Cryptographic Boolean Functions and Applications // Academic Press is an imprint of Elsevier 525 В Street, Suite 1900, San Diego, CA 92101-4495, USA Linacre House, Jordan Hill, Oxford OX2 8DP, UK. First edition, 2009 - 345 p.
4. .4. Зубов А.Ю., Совершенные шифры. М.: Гелиос АРВ, 2003. - 1бос.
5. Криптография и алгоритмы шифрования - [Электронный ресурс]// URL: http://vse-shiiri.ru/.
6. Bruce Schneier. Applied Cryptography// Second Edition: Protocols, Algorthms, and Source Code in С (cloth), 1996 - 234 p.